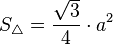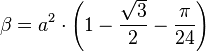DataLife Engine - Softnews Media Group

Построение треугольника Рёло

Треуго́льник Рёло представляет собой область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне^[1][2]. Негладкая замкнутая кривая, ограничивающая эту фигуру, также называется треугольником Рёло.

Треугольник Рёло является простейшей после круга фигурой постоянной ширины^[1]. То есть если к треугольнику Рёло провести пару параллельных опорных прямых^{[* 2]}, то независимо от выбранного направления расстояние между ними будет постоянным^[3]. Это расстояние называется шириной треугольника Рёло.

Среди прочих фигур постоянной ширины треугольник Рёло выделяется рядом экстремальных свойств: наименьшей площадью^[1], наименьшим возможным углом при вершине^[4], наименьшей симметричностью относительно центра^[5]. Треугольник получил распространение в технике — на его основе были созданы кулачковые и грейферные механизмы, роторно-поршневой двигатель Ванкеля и даже свёрла, позволяющие сверлить квадратные отверстия^[6].

Название фигуры происходит от фамилии немецкого механика Франца Рёло. Он, вероятно, был первым, кто исследовал свойства этого треугольника; также он использовал его в своих механизмах^[7].

[править]История

Mappamundi. Леонардо да Винчи, примерно 1514 год

Рёло не является первооткрывателем этой фигуры, хотя он и подробно исследовал её. В частности, он рассматривал вопрос о том, сколько контактов (в кинематических парах) необходимо, чтобы предотвратить движение плоской фигуры, и на примере искривлённого треугольника, вписанного в квадрат, показал, что даже трёх контактов может быть недостаточно для того, чтобы фигура не вращалась^[8].

Леонардо да Винчи, манускрипт A, фрагмент листа 15v

Некоторые математики считают, что первым продемонстрировал идею треугольника из равных дуг окружности Леонард Эйлер в XVIII веке^[9]. Тем не менее, подобная фигура встречается и раньше, в XV веке: её использовал в своих рукописях Леонардо да Винчи. Треугольник Рёло есть в его манускриптах A и B, хранящихся в Институте Франции^[10], а также в Мадридском кодексе^[9].

Примерно в 1514 году Леонардо да Винчи создал одну из первых в своём роде карт мира. Поверхность земного шара на ней была разделена экватором и двумя меридианами (угол между плоскостями этих меридианов равен 90°) на восемь сферических треугольников, которые были показаны на плоскости карты треугольниками Рёло, собранными по четыре вокруг полюсов^[11].

Ещё раньше, в XIII веке, создатели церкви Богоматери в Брюгге использовали треугольник Рёло в качестве формы для некоторых окон^[9].

[править]Свойства

Треугольник Рёло является плоской выпуклой геометрической фигурой^[12].

[править]Основные геометрические характеристики

Если ширина треугольника Рёло равна , то его площадь равна^[13]

периметр

радиус вписанной окружности

а радиус описанной окружности

.

[править]Симметрия

Треугольник Рёло обладает осевой симметрией. Он имеет три оси симметрии второго порядка, каждая из которых проходит через вершину треугольника и середину противоположной дуги, а также одну ось симметрии третьего порядка, перпендикулярную плоскости треугольника и проходящую через его центр^{[* 3]}. Таким образом, группа симметрий треугольника Рёло состоит из шести отображений (включая тождественное) и совпадает с группой 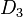 симметрий правильного треугольника.

[править]Построение циркулем

Треугольник Рёло можно построить с помощью одного только циркуля, не прибегая к линейке. Это построение сводится к последовательному проведению трёх равных окружностей. Центр первой выбирется произвольно, центром второй может быть любая точка первой окружности, а центром третьей — любая из двух точек пересечения первых двух окружностей.

[править]Свойства, общие для всех фигур постоянной ширины

Поскольку треугольник Рёло является фигурой постоянной ширины, он обладает всеми общими свойствами фигур этого класса. В частности,

• с каждой из своих опорных прямых треугольник Рёло имеет лишь по одной общей точке^[14];
• расстояние между двумя любыми точками треугольника Рёло ширины  не может превышать ^[15];
• отрезок, соединяющий точки касания двух параллельных опорных прямых к треугольнику Рёло, перпендикулярен к этим опорным прямым^[16];
• через любую точку границы треугольника Рёло проходит по крайней мере одна опорная прямая^[17];
• через каждую точку  границы треугольника Рёло проходит объемлющая его окружность радиуса ^{[* 4]}, причём опорная прямая, проведённая к треугольнику Рёло через точку , является касательной к этой окружности^[18];
• радиус окружности, имеющей не меньше трёх общих точек с границей треугольника Рёло ширины , не превышает ^[19];
• по теореме Ханфрида Ленца^[ru] о множествах постоянной ширины треугольник Рёло нельзя разделить на две фигуры, диаметр которых был бы меньше ширины самого треугольника^[20][21];
• треугольник Рёло, как и любую другую фигуру постоянной ширины, можно вписать в квадрат^[22], а также в правильный шестиугольник^[23];
• по теореме Барбье формула периметра треугольника Рёло справедлива для всех фигур постоянной ширины^[24][25][26].

[править]Экстремальные свойства

[править]Наименьшая площадь

Среди всех фигур постоянной ширины  у треугольника Рёло наименьшая площадь^[1]. Это утверждение носит название теоремы Бляшке — Лебега^[27][28] (по фамилиям немецкого геометра Вильгельма Бляшке, опубликовавшего теорему в 1915 году^[29], и французского математика Анри Лебега, который сформулировал её в 1914 году^[30]). В разное время варианты её доказательства предлагали Мацусабуро Фудзивара (1927 и 1931 год)^[31][32], Антон Майер (1935 год)^[33], Гарольд Эгглстон (1952 год)^[34], Абрам Безикович (1963 год)^[35], Дональд Чакериан (1966 год)^[36], Эванс Харрелл (2002 год)^[37] и другие математики^[5].

Чтобы найти площадь треугольника Рёло, можно сложить площадь внутреннего равностороннего треугольника

и площадь трёх оставшихся одинаковых круговых сегментов, опирающихся на угол в 60°

то есть

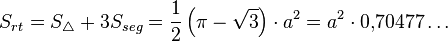^[38]

Фигура, обладающая противоположным экстремальным свойством — круг. Среди всех фигур данной постоянной ширины его площадь

максимальна^{[39][* 5]}. Площадь соответствующего треугольника Рёло меньше на ≈10,27 %. В этих пределах лежат площади всех остальных фигур данной постоянной ширины.

[править]Наименьший угол

Через каждую вершину треугольника Рёло, в отличие от остальных его граничных точек, проходит не одна опорная прямая, а бесконечное множество опорных прямых. Пересекаясь в вершине, они образуют «пучок». Угол между крайними прямыми этого «пучка» называетсяуглом при вершине. Для фигур постоянной ширины угол при вершинах не может быть меньше 120°. Единственная фигура постоянной ширины, имеющая углы, равные в точности 120° — это треугольник Рёло^[4].

[править]Наименьшая центральная симметрия

Треугольник Рёло (коричневый) и его образ при центральной симметрииотносительно своего центра (заштрихован). Наибольшая центрально-симметричная фигура, в нём содержащаяся (криволинейный шестиугольник), и наименьшая центрально-симметричная, его содержащая (правильный шестиугольник) выделены жирной линией

Из всех фигур постоянной ширины треугольник Рёло обладает центральной симметрией в наименьшей степени^{[5][40][41][42][43]}. Существует несколько различных способов дать определение степени симметричности фигуры. Один из них — это мера Ковнера — Безиковича. В общем случае для выпуклой фигуры  она равна

где  — площадь фигуры,  — содержащаяся в  центрально-симметричная выпуклая фигура максимальной площади. Для треугольника Рёло такой фигурой является шестиугольник с искривлёнными сторонами, представляющий собой пересечение этого треугольника Рёло со своим образом при центральной симметрии относительно своего центра^{[* 3]}. Мера Ковнера — Безиковича для треугольника Рёло равна

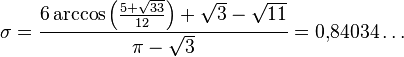^[5][40]

Другой способ — это мера Эстерманна

где  — содержащая  центрально-симметричная фигура минимальной площади. Для треугольника Рёло  — это правильный шестиугольник, поэтому мера Эстерманна равна

^[5][36]

Для центрально-симметричных фигур меры Ковнера — Безиковича и Эстерманна равны единице. Среди фигур постоянной ширины центральной симметрией обладает только круг^[25], который (вместе с треугольником Рёло) и ограничивает область возможных значений их симметричности.

[править]Качение по квадрату

Качение треугольника Рёло по квадрату

Любая фигура постоянной ширины вписана в квадрат со стороной, равной ширине фигуры, причём направление сторон квадрата может быть выбрано произвольно^{[22][* 6]}. Треугольник Рёло — не исключение, он вписан в квадрат и может вращаться в нём, постоянно касаясь всех четырёх сторон^[44].

Каждая вершина треугольника при его вращении «проходит» почти весь периметр квадрата, отклоняясь от этой траектории лишь в углах — там вершина описывает дугу эллипса. Центр этого эллипса расположен в противоположном углу квадрата, а его больша́я и малая оси повёрнуты на угол в 45° относительно сторон квадрата и равны

где  — ширина треугольника^[45]. Каждый из четырёх эллипсов касается двух смежных сторон квадрата на расстоянии

от угла^[38].

Эллипс (выделен красным цветом), очерчивающий один из углов фигуры (её граница выделена чёрным цветом), которую покрывает треугольник Рёло при вращении в квадрате	Угол покрываемой вращением фигуры. Подписаны точки касания сторон квадрата с эллипсом. Светло-жёлтым показан не затронутый вращением угол квадрата

Центр треугольника Рёло при вращении движется по траектории, составленной из четырёх одинаковых дуг эллипсов. Центры этих эллипсов расположены в вершинах квадрата, а оси повёрнуты на угол в 45° относительно сторон квадрата и равны

^[45].

Иногда для механизмов, реализующих на практике такое вращение треугольника, в качестве траектории центра выбирают не склейку из четырёх дуг эллипсов, а близкую к ней окружность^[46].

Эллипс (выделен красным цветом), очерчивающий одну четвёртую кривой, по которой движется центр треугольника Рёло при вращении в квадрате	Траектория центра треугольника Рёло при вращении в квадрате. Выделены точки сопряжения четырёх дуг эллипсов. Для сравнения показана окружность (синим цветом), проходящая через эти же четыре точки

Площадь каждого из четырёх не затронутых вращением уголков равна